The 360° Pendulum
Normally we think of a pendulum as a
weight suspended by a flexible string or cable, so that it may swing back and
forth. Another type of pendulum
consists of a weight attached by a light (but inflexible) rod to an axle, so
that it can swing through larger angles, even making a 360° rotation if given
enough velocity.
Though
it is not precisely correct in practice, we often assume that the magnitude of
the frictional forces that eventually slow the pendulum to a halt is
proportional to the velocity of the pendulum.
Assume also that the length of the pendulum is 1 meter, the weight at
the end of the pendulum has mass 1 kg, and the coefficient of friction is
0.5. In that case, the equations of
motion for the pendulum are as follows.
x'(t)
= y(t), y'(t) = – 0.5y(t) – 9.81sin(x(t)),
where t represents time in seconds, x
represents the angle of the pendulum from the vertical in radians (so that x
= 0 is the rest position), y
represents the velocity of the pendulum in radians per second, and 9.81 is
approximately the acceleration due to gravity in meters per second
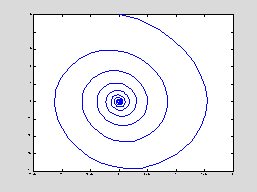
squared. Now here is a phase portrait
of the solution with initial position x0 = 0 and initial velocity y0
= 5. This is a graph of x versus y as a function of t. on the time interval 0 £ t
£ 20.
g =
inline('[x(2); -0.5*x(2) - 9.81*sin(x(1))]', 't', 'x');
[t, xa] = ode45(g, [0 20], [0 5]);
plot(xa(:, 1), xa(:, 2))
Recall that the x coordinate corresponds to the angle of the pendulum and the y coordinate corresponds to its
velocity. Starting at (0,5), as t increases we follow the curve as it
spirals clockwise toward (0,0). The
angle oscillates back and forth, but with each swing it gets smaller until the
pendulum is virtually at rest by the time t = 20.
Meanwhile the velocity oscillates as well, taking its maximum value
during each oscillation when the pendulum is in the middle of its swing (the
angle is near zero) and crossing zero when the pendulum is at the end of its
swing.
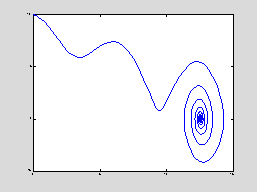
Next we increase the initial velocity
to 10.
[t, xa] =
ode45(g, [0 20], [0 10]);
plot(xa(:,1), xa(:,2))
This time the angle increases to over
14 radians before the curve spirals in to a point near (12.5,0). More precisely, it spirals toward (4p, 0), because 4p radians represents the same position
for the pendulum as 0 radians does. The
pendulum has swung overhead and made two complete revolutions before beginning
its damped oscillation toward its rest position. The velocity at first decreases but then rises after the angle
passes through p, as the
pendulum passes the upright position and gains momentum. The pendulum has just enough momentum to
swing through the upright position once more at the angle 3p.
Now suppose we want to find, to within 0.1, the minimum initial velocity required to make the pendulum,
starting from its rest position, swing overhead once. It will be useful to be able to see the solutions corresponding
to several different initial velocities on one graph.
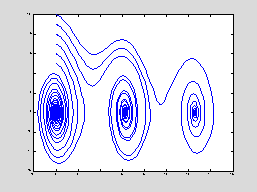
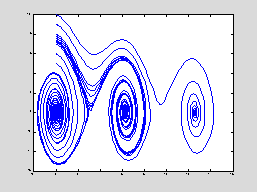
First we consider the integer
velocities 5 to 10.
for a = 5:10
[t, xa] = ode45(g, [0 20],
[0 a]);
plot(xa(:, 1), xa(:, 2))
end
hold off
Initial velocities 5, 6, 7 are not
large enough for the angle to increase past p, but initial velocities 8, 9, 10 are enough to make the pendulum swing
overhead. Let's see what happens
between 7 and 8.
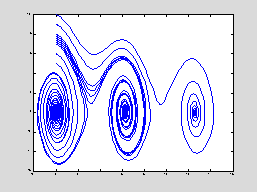
for a = 7.0:0.2:8.0
[t, xa] = ode45(g, [0 20],
[0 a]);
plot(xa(:, 1), xa(:, 2))
end
hold off
We see that the cut-off is somewhere
between 7.2 and 7.4. Let's make one
more refinement.
for a = 7.2:0.05:7.4
[t, xa] = ode45(g, [0 20],
[0 a]);
plot(xa(:, 1), xa(:, 2))
end
hold off
We conclude that the minimum velocity
needed is somewhere between 7.25 and 7.3.