Airy's equation compared with ``facsimile" equations
clear all close all
Solution near t=0. Here is the correct way to enter Airy's equation.
airy = @(t, y) [y(2); t*y(1)]; [tfor, yfor] = ode45(airy, [0,2], [0,1]); plot(tfor, yfor(:,1), 'r') hold on [tbak, ybak] = ode45(airy, [0,-2], [0,1]); plot(tbak, ybak(:,1), 'r') facA = dsolve('D2y = 0', 'y(0)=0', 'Dy(0)=1') ezplot(facA, [-2, 2]) hold off title(['solution to Airy\prime', 's equation and facsimile near t=0'])
facA = t
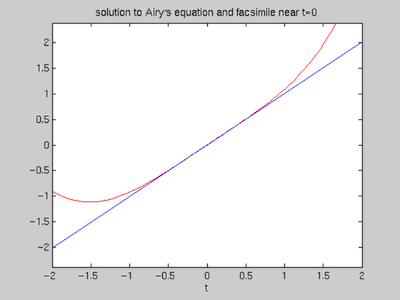
The facsimile agrees well with the actual solution in a neighborhood of the origin.
Solution for t near -16 = -4^2.
solb = ode45(airy, [0,-20], [0,1]); tt = -18:.05:-14; yy = deval(solb, tt, 1); plot(tt, yy, 'r') hold on
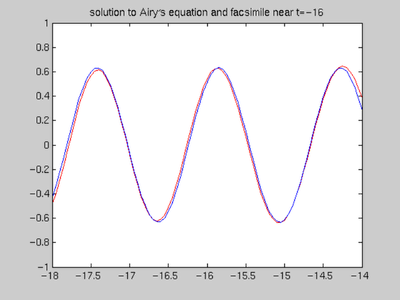
After viewing the graph, we see that it does resemble a sine curve. Now the solutions of y'' = -16*y are spanned by sin(4*t) and cos(4*t). So we want to find the best values of a(1) and a(2) for which yy ~ a(1)*sin(4*tt) + a(2)*cos(4*tt) We can do this with MATLAB's "backslash" command, as discussed in sections 4.1.3 and 8.4.
a = [sin(4*tt) ; cos(4*tt)]' \ yy' facB = a(1)*sin(4*tt) + a(2)*cos(4*tt); plot(tt, facB, 'b') hold off axis([-18 -14 -1 1]) title(['solution to Airy\prime', ... 's equation and facsimile near t=-16'])
a =
-0.3360
0.5358
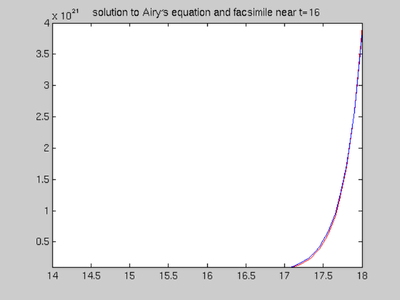
Solution for t near 16 = 4^2.
solf = ode45(airy, [0,18], [0,1]); tt = 14:.05:18; yy = deval(solf, tt, 1); plot(tt, yy, 'r') hold on axis([14 18 10^20 4*10^21])
After viewing the graph, we see that it does resemble a hyperbolic sine curve. Now the solutions of y'' = -16*y are spanned by sinh(4*t) and cosh(4*t). So we want to find the best values of a(1) and a(2) for which yy ~ a(1)*sinh(4*tt) + a(2)*cosh(4*tt) We can do this with MATLAB's "backslash" command, as discussed in sections 4.1.3 and 8.4.
a = [sinh(4*tt) ; cosh(4*tt)]' \ yy' facC = a(1)*sinh(4*tt) + a(2)*cosh(4*tt); plot(tt, facC, 'b') hold off axis([14 18 10^20 4*10^21]) title(['solution to Airy\prime', ... 's equation and facsimile near t=16'])
Warning: Rank deficient, rank = 1, tol = 2.9111e+17.
a =
1.0e-09 *
0.4160
0
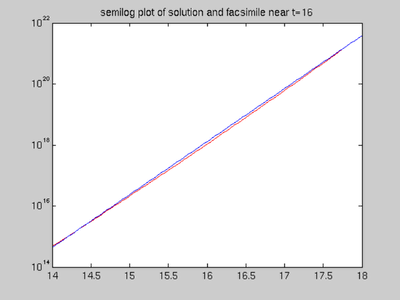
Since the solution is so large, we can get a better picture with a semilogarithmic plot. Recall that a semilog plot of an exponential function looks almost like a straight line.
semilogy(tt, yy, 'r', tt, facC, 'b') title('semilog plot of solution and facsimile near t=16')

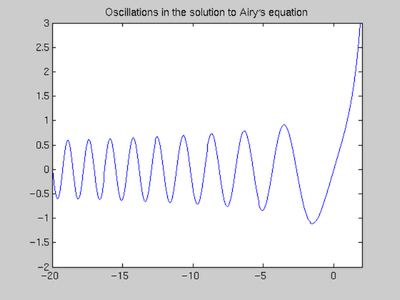
Solution over (-20,2), oscillations for negative time
ttb = -20:0.05:0; yyb = deval(solb, ttb, 1); ttf = 0:0.05:2; yyf = deval(solf, ttf, 1); plot(ttb, yyb, 'b', ttf, yyf, 'b') axis([-20 2 -2 3]) title(['Oscillations in the solution to Airy\prime', ... 's equation'])

It appears that the frequency increases and the amplitude decreases as t goes to minus infinity. The increasing frequency is predicted by our analysis; the decreasing amplitude is harder to explain.